光的电磁波理论(二)

电磁波与辐射

电偶极子

振荡的电偶极子：外界能量激发下，正负电中心不在一起，距离产生变化，并伴随着交变的电磁场->能量传递
电偶极子作简谐振荡时，电偶极矩 $\vec{p}=\vec{p_0}e^{-i\omega t}$
远离电偶极子中心的点M处的场为：

$\vec{E}=\cfrac{\omega^2(\vec{r}\times\vec{p_0})\times\vec{r}}{4\pi\epsilon v^2r^3}exp[i(kr-\omega t)]$

$\vec{E}=\cfrac{\omega^2(\vec{r}\times\vec{p_0})}{4\pi\epsilon v^3r^2}exp[i(kr-\omega t)]$

从中可以观测到两者的关系为：

$\vec{E}=\frac{v}{r}(\vec{B}\times\vec{r})$

实际光波

波列是一种相速度基本相同，传播方向相同的波的叠加，在任意时刻，可以用周期函数来描述。谐波是用调和函数来描述的无限延伸波列。
实际光波是在时空中存在衰减振动，并且波列是由原子间的碰撞产生的（例如激光上下能级跃迁），存在时间约 $\leq10^{-8}$ s，且不存在偏振特性
目前所称的光波，是指在T时刻内接收的光波列的组合，振动方向和相位被平均。

辐射能

电磁波的传播伴随能量的传递，空间中区域的单位体积辐射能称为能量密度，可表示为：

$\omega=\frac{1}{2}(\vec{E}\cdot\vec{D}+\vec{H}\cdot\vec{B})=\frac{1}{2}(\epsilon E^2+\frac{1}{\mu}B^2)$

能流密度是指单位时间内垂直通过的单位面积的能量，用于描述电磁场能量的传播，用坡印廷矢量表示：

$\vec{S}=\omega v=\frac{1}{\mu}\vec{E}\times\vec{B}$

光强为： $I=\langle s\rangle=\frac{1}{2}\sqrt{\frac{\epsilon}{\mu}}A^2$
在同一均匀介质下 ,两点的场强的相对强度可用A的平方表示，当使用复振幅表示时为：

$I=\tilde{E}\cdot\tilde{E}^\ast$

光在介质分界面上的折射和反射

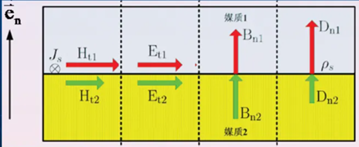
连续性条件

电磁波由一种介质传导到另一种介质，折射率的改变导致电磁场在界面上不连续。在无源场的界面上，磁感应强度B和电感应强度D法向分量连续；磁场强度E和电场强度H切向分量连续。
界面连续性

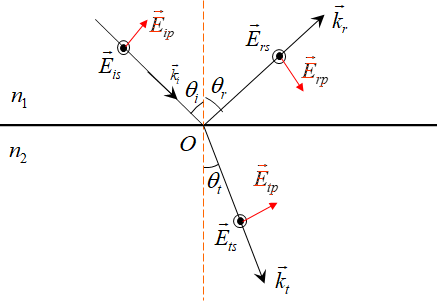
菲涅尔公式与折反射

通常把垂直于入射面振动的分量叫做s分量，把平行于入射面（在入射面内）振动的分量称做p分量，如图所示。
振动分量
连续性图
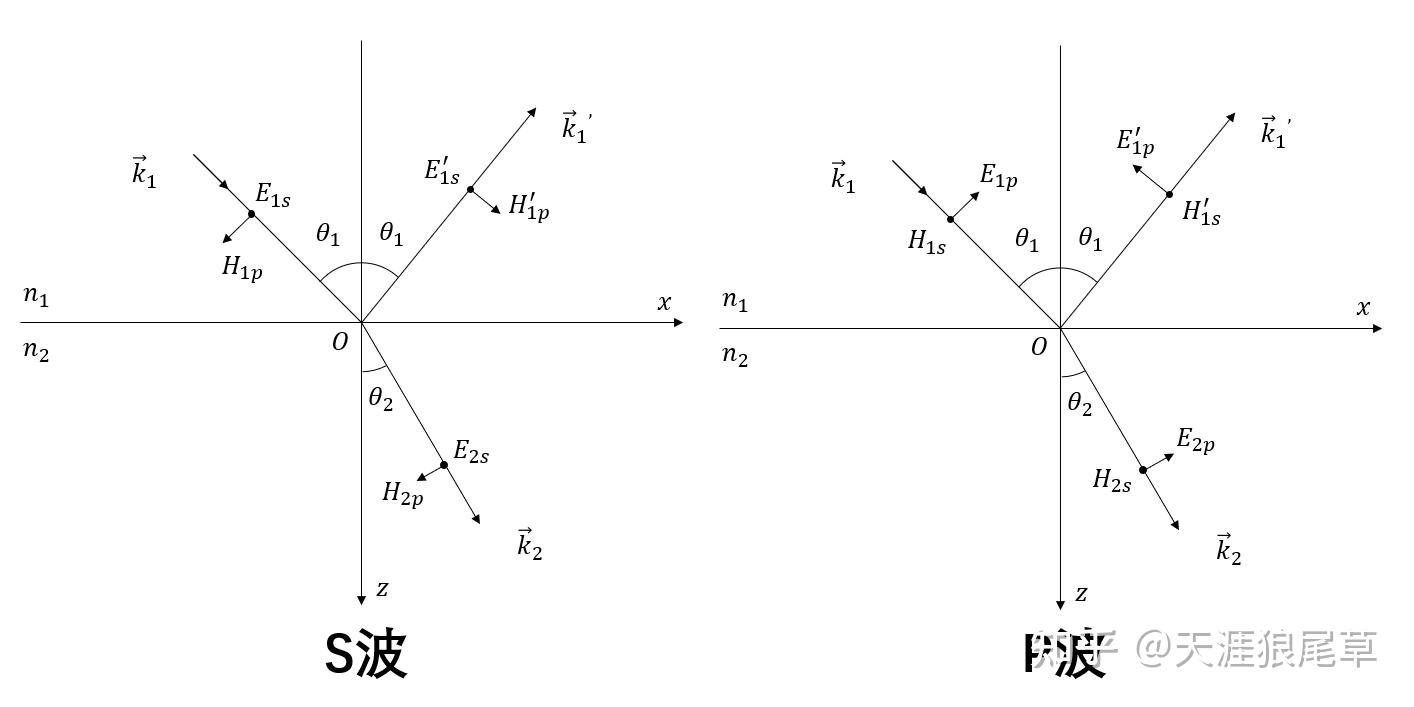
从连续性条件可知：

$E_{is}+E_{rs}=E_{ts}$

$H_{ip}cos\theta_i-H_{rp}cos\theta_r=H_{tp}cos\theta_t$

$H_{is}+H_{rs}=H_{ts}$

$E_{ip}cos\theta_i-E_{rs}cos\theta_r=E_{ts}cos\theta_t$

通过 $\vec{H}=\frac{n}{\mu}(\vec{k_0}\times\vec{E})$ ，可得到

$r_s=\frac{A_{rs}}{A_{is}}=\frac{E_{rs}}{E_{is}}=\cfrac{n_1/\mu_1*cos\theta_1-n_2/\mu_2*cos\theta_2}{n_1/\mu_1*cos\theta_1+n_2/\mu_2*cos\theta_2}$

$t_s=\frac{A_{ts}}{A_{is}}=\frac{E_{ts}}{E_{is}}=\cfrac{2*n_1/\mu_1*cos\theta_1}{n_1/\mu_1*cos\theta_1+n_2/\mu_2*cos\theta_2}$

$r_p=\frac{A_{rp}}{A_{ip}}=\frac{E_{rp}}{E_{ip}}=\cfrac{n_2/\mu_2*cos\theta_1-n_1/\mu_1*cos\theta_2}{n_2/\mu_2*cos\theta_1+n_1/\mu_1*cos\theta_2}$

$t_p=\frac{A_{tp}}{A_{ip}}=\frac{E_{tp}}{E_{ip}}=\cfrac{2*n_1/\mu_1*cos\theta_1}{n_2/\mu_2*cos\theta_1+n_1/\mu_1*cos\theta_2}$

当两种介质都为电介质时，一般考虑非磁性物质情况，认为磁导率相同，即： $\mu_1=\mu_2$ ,可进一步简化上式：

$r_s==\cfrac{n_1cos\theta_1-n_2cos\theta_2}{n_1cos\theta_1+n_2cos\theta_2}=-\frac{sin(\theta_1-\theta_2)}{sin(\theta_1+\theta_2}$

$t_s=\cfrac{2n_1cos\theta_1}{n_1cos\theta_1+n_2cos\theta_2}=\frac{2sin\theta_2cos\theta_1}{sin(\theta_1+\theta_2)}$

$r_p==\cfrac{n_2cos\theta_2-n_1cos\theta_1}{n_2cos\theta_1+n_1cos\theta_2}=\frac{tan(\theta_1-\theta_2)}{tan(\theta_1+\theta_2}$

$t_s=\cfrac{2n_1cos\theta_1}{n_2cos\theta_1+n_1cos\theta_2}=\frac{2sin\theta_2cos\theta_1}{sin(\theta_1+\theta_2)cos(\theta_1-\theta_2)}$

简化方法为同时除以 $n_2$ ，然后通过折射定律替换成展开的两角和公式。